… A summary by Vinay Wagh
We carry a common myth that most of the Math that is being taught in the schools and colleges is useless. But that’s not true. Math was formulated to satisfy the needs of previous centuries and is now used to handle the modern technologies. The way math was formulated and is being used is meticulously answered in this book by Steven in an interesting way that truly connects practical life
Why sum of the n odd natural numbers is n2?
1 + 3 = 22, 1 + 3 + 5 =32 and 1+ 3 + 5 = 42…and so on
Why is the sum of n natural numbers n(n+1)/2?
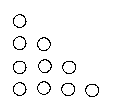
1+2 +3 + 4 is?
Put white marbles on the floor in the given order. 1, then 2, then 3 and then 4. Now make a rectangle by adding black marbles. Now it becomes a rectangle of four rows and five columns. (4 x 5). There are 20 marbles. So how many are white? Half of 20 = 10. Area of triangle is half of the area of rectangle. So n(n+1)/2

The enemy of my enemy: Negativity multiplied by negativity turns it into positivity.
Scholars have used these ideas to analyze the run-up to world war-I. It shows the shifting alliances from Great Britain, France, Russia, Italy, Germany, Austria and Hungary between 1872 and 1907. The bold segment between the countries shows friendly relationship. The dotted segment indicates Hostile relationship.
The bold line represents friendly relation whereas the dotted line indicates enmity
Some part of what we observe is due to nothing more than the primitive logic of “The enemy of my enemy” and this part is captured perfectly by the multiplication of negative numbers.
Commutative law application:
- 10 % Tax to be applied after a discount of 20%
- 20% discount to be applied on a value that is increased by 10% tax.
Although it is the same, quite a few find it different. You will end getting 12% decrease on the given marked price. All it says is a x b = b x a
The commutative law does not always work with our mindsets. Let’s say that a person wants to get into IIM-B very desperately. Not getting there can lead her to take a silly step of committing suicide. The person gets rejected by IIM-B but gets a call from IIM-C. The girl cancels the idea of committing suicide. She can go to IIM-C and commit suicide, but not the other way round.
Early in the development of quantum mechanics, Werner Heisenberg and Paul Dirac had discovered that nature follows a curious kind of logic in which p x q ≠ q x p where p and q represent the momentum and position of quantum particle. Without that break-down of commutative law, there would be no Heisenberg uncertainty principle, atoms would collapse and nothing would exist. That’s why you better mind your p’s and q’s.
Division and its Discontents:
0.12122122212222…..
By design, the blocks of 2 get progressively longer as we move to the right. There is no way to express this decimal fraction. It’s irrational!
The joy of x
Grant wiggins, an education consultant, has been posing a problem to students and faculties for years. More than 50% people got it wrong.
Try and make an equation for a relation, “One yard equals three feet”.
If you think the answer is 1 y = 3f, welcome to the club of 50%. Seems to be a straightforward translation but as soon as you try a few numbers, you’ll see that this formula does not work. Say the hallway is 10 yards long. We all know it is 30 feet. Now plug y = 10 and f =30 the formula does not work.
The correct equation is f = 3y. Here 3 really means “3 feet per yard”. When you multiply it by Y in yards, the units of yards cancel out and you’re left with units of feet, as you should be.
Imagine imaginary numbers
What multiplying by i (imaginary number) looks like?
Multiplying by ‘I’ produces a rotation counterclockwise by a quarter turn. It takes an arrow of length 2 pointing east and changes it into a new arrow of the same length but now pointing north. Electrical engineers love complex numbers for exactly this reason. Having such a compact way to represent 90o rotations is very useful when working with Alternating currents and magnetic fields, because these often involve oscillations or waves that are quarter cycles. In aerospace engineering they eased the first calculations of the lift on an aero plane wing. Civil and mechanical engineers use them routinely to analyze the vibrations of footbridge, skyscrapers and cars driving on bumpy roads.
The 90o rotation property also sheds light on what i2 = -1 really means. If we multiply positive number by i2, the corresponding arrow rotates 180o, flipping the arrow from east to west.
Why the name Algebra?
In the early part of ninth century, Muhammad bin Musa al-Khwarizmi, a mathematician working in Baghdad, wrote a seminal text book in which he highlighted the usefulness of restoring a quantity being subtracted by being added to the other side of equation. Say x + 2 = 4. We subtract 2 on both sides to get x +2 -2 = 4 -2. So x = 2. He called this process as Al-jabr (Arabic word for ‘restoring’) which later morphed into ‘Algebra”. Then long after his death, he hit the etymological jackpot again. His own name, Al- khwarizmi, lives on today in word, “Algorithm”.
Quadratic Equations
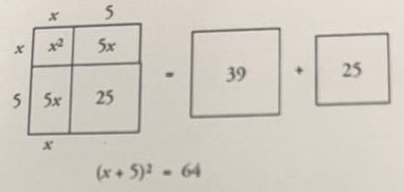
X2 + 10 x = 39
Al-Khwarizmi put the puzzle this way X2 + 10x = 39

The missing corner was an irresistible step. That was filled in to turn the figure into a perfect square.
Power tools
A mathematician needs Functions for the same reason that a builder needs hammers and drills. Tools transform things. So does functions.
If we plot y = 4 –x2 on graph we get
The bowed shape of the curve is due to the action of mathematical pliers. The function that transforms x into x2 behaves a lot like the common tool for bending and pulling things. And what role does the 4 play in the equation? It acts like a nail for hanging a picture on a wall. It lifts the bent wire arch by 4 units. Since it raises all the points by the same amount it’s known as a constant function. The tool x2 bends the piece of X-axis and the ‘4’ lifts it and holds it. These building blocks 4 and -x2 can be regarded as component parts of a more complicated function, 4- x2, just as wires, batteries and transistors are components of a radio. If you look this way, you’ll start noticing functions everywhere.
Power functions of the form xn in which the variable x is raised to a fixed power n. changing n yields handy tools. For parabola n = 2 and for constant n = 0. Whereas n =1 gives a function that works like a ramp, a steady incline or a decline. It’s called linear function as it produces a line on the graph. What it n = -2? (1/x2). This function is good to describe how waves and forces attenuate as they spread out in three dimensions the way sound softens as it moves away from the source.
A Paper can be folded only seven to eight times.
In x2, as x gets larger and larger an exponential function of x eventually grows faster than any power function no matter how large the power. Exponential growth in almost unimaginably rapid. That’s why it’s so hard to fold a piece of paper in half more than seven or eight times. Each folding approximately doubles the thickness of the wad, causing it to grow exponentially. Meanwhile the Wad’s length shrinks in half every time and thus decreases exponentially fast. For standard sheet of the note book paper, the wad becomes thicker than it is long and so it can’t be folded again. For a sheet to be considered legitimately folded n times, the resulting wad is required to have 2n layers in a straight line, and this can’t happen if the wad is thicker than it is long. In 2002 Britney Gallivan, then a junior in high school solved. She made a formula that predicted the maximum number of times, n, that paper of a given thickness T and length L could be folded in one direction.
L = T6 (2n + 4)( 2n – 1).
The conic Conspiracy:
Whispering galleries are remarkable acoustic spaces found beneath certain domes, vaults or curved ceilings. There is famous whispering gallery in New York, the Grand central station. It’s a fun place to take a date. You can communicate by whispering when you are forty feet apart and separated by a bustling passageway. You’ll hear each other clearly but the passersby won’t hear a word you’re saying.
To produce this effect, the two of you should stand at diagonally opposite corners of the space, facing the wall. That puts you each near a focus, a special point at which the sound of your voice gets focused as it reflects off the passageway’s curved walls and ceiling. Ordinarily, the sound waves you produce travel in all the directions and bounce off the walls at disparate times and places, scrambling them so much that they are inaudible when they arrive at the ear of listener forty feet away (which is why the passersby can’t hear what you’re saying). But when you whisper at the focus, the reflected waves all arrive at the same time at the other focus, thus reinforcing one another and allowing your words to be heard.
Ellipse:
Ellipse displays a similar flair for focusing, though in a much simpler form. If we fashion a reflector in the shape of an ellipse, two particular points inside it (marked as F1 and F2) will act as foci in the following sense: All the rays emanating from a light source at one of those points will be reflected to the other.

Or if pool is to be paled on an elliptical table, with the pocket on one of the focus, there is an interesting trick that can be used in playing. To set up the trick shot that is guaranteed to scratch every time, place the cue ball at the other focus. No matter where you strike the ball and no matter where it caroms off the cushion, it will always go to the pocket.
This focusing property of parabolas is just as useful when deployed in reverse. Suppose we want to make a strongly directional beam of light, like that needed for spotlight of car headlights. On its own, a bulb – even a powerful one typically wouldn’t be good enough; it wastes too much of light by shining in all the directions. But now place the bulb at the focus of a parabolic reflector and voila! The parabola creates a directional beam automatically. It takes the bulbs rays and, by reflecting them off the parabola’s silvered inner surface, makes them all parallel.
As Parabola is a set of points equidistant from given point and a given line (directrix) not containing that point the convergence of the light rays becomes obvious.
The reason for calling F the focus becomes clear if we think of the parabola as a curved mirror. It turns out that if you shine a beam of light straight at a parabolic mirror all the reflected rays will intersect simultaneously at point F producing an intensely focused spot of light.
Mathematicians and the conspiracy theorists have this much in common: We’re suspicious of coincidences – especially the convenient ones. There are no accidents.
Why Parabola and ellipse only have such a fantastic powers of focusing?
They are both cross-sections of the surface of Cone. So cone is the mother of Circle, ellipse, parabola and Hyperbola together called conic section. In algebra together they arise as the graphs of second degree equations
Ax2 + Bxy + Cy2 + DX+ EY + F =0
The constants A,B,C,D,E and F determine whether the graph is a circle, ellipse, parabola or a hyperbola. So it’s no accident that planets move in elliptical orbits with the sun at one focus; or that comets sail through the solar system on elliptic, parabolic or hyperbolic trajectories; or that a child’s ball tossed to parent follows a parabolic arc. They’re all manifestations of the conic conspiracy.
Conversion of circular motion into sine waves is a pervasive though often unnoticed is a part of our daily experience. It creates hum of the florescent lights overhead in our offices, a reminder that somewhere in the power grid, generators are spinning sixty cycles per second, converting the rotary motion into alternating current, the electrical sine waves on which the modern life depends. When you speak and I hear, both our bodies are using sine waves- yours in the vibrations of your vocal cords to produce the sounds and mine in the swaying of hair cells in my ears to receive them.
Change we can believe in
Imagine a mechanically controlled bank of anti-craft guns automatically firing at an incoming fighter plane. Calculus, tells the guns where to aim. Calculus is the mathematics of change. It describes everything from the epidemics to the Zigs and Zags of well-thrown curveball. Roughly, the derivative tells you how fast something is changing’; the integral tells you how much it’s accumulating. They were born in separate times and places. Integrals in Greece around 250 BC and Derivatives in England and Germany in the md-1600’s.Yet they’ve turned out to be blood-relatives.
Change is the most sluggish at the extremes, precisely because the derivative is zero there. Things stand still momentarily. This zero derivative property of crests and troughs underlies some of the most practical applications of calculus. It allows us to use derivatives to figure out where a function reaches its maximum or minimum, an issue that arises whenever we are looking for the best or the cheapest or the fastest way to do something.
In integration the symbol ‘∫’ simply means along ‘S’ that stands for sum. In astronomy, the gravitational pull of the sun on the Earth is described by an Integral. It represents a collective effect of all the miniscule forces generated by each solar atom at the varying distances from the earth. In oncology, the growing mass of solid tumor can be modeled by an integral. Why Sums like this require Integration and not the school methods of adding? The first reason is that neither Sun nor Earth are points. Both are gigantic balls made up of stupendous number of atoms. Every atom in the sun exerts gravitational tug on every atom on the earth. Of course, since atoms are tiny, their mutual attractions are almost infinitesimally small. But there are infinitely many of them, in aggregate they can still amount to something. Somehow we have to add them all up.
All about ‘e’
A few numbers are such celebrities that they go by single-letter stage names, something not even Amitabh Bachhan or Sachin Tendulkar can match. The most famous is π, the number that represents the ratio of the circumference to the diameter of a circle. Closely behind is ‘i’ the imaginary number so radical that it changed what it meant to be a number. Who’s the next celebrity?
Now say hello to ‘e’ nicknamed for its breakout role in exponential growth, e is now the Zelig of advanced Mathematics. From the insights it offers about chain reactions and population booms, e has a thing or two to say about how many people you should debate before settling down.
What’s e?
It is a numerical value 2.71828….
To make it simpler, understand this..
1+ 11 + 11×2 + 11x2x3 + 11x2x3x4 + ….
Imagine that you’ve deposited `1000 in a savings account that offers 100% interest rate compounded annually. A year later your amount should be `2000. What if you ask the bank to pay 50% semiannually instead of 100% annually? You’ll get better than before. It will be
1000 + 500 =1500 and then 1500 + 750 = 2250. What if you further negotiate and ask the bank to break further and further? Like 25% per quarter then, then monthly…soon till hours, mins, secs or even Nano-seconds. Would you make a small fortune of sorts?
To make the numbers come out nicely, here’s the result for a year divided into hundred equal periods, after each of which you’d be paid 1percent interest (The 100% annual rate divided evenly into 100 installments) your money would grow by a factor of 1.01raised to100th power and that comes out to be about 2.70481….In other words the `1000 would be come `20704.81…
But what if the interest is compounded infinitely often?
This is called as continuous compounding and your total after one year would be `2718.28…
So e = 1+1nn = 2.71828….
Differential equation for Romeo and Juliet
How does their love ebb and flow over time? That’s where calculus comes in. By writing equations that summarize how Romeo and Juliet respond to each other’s affections and then solving those equations with calculus, we can predict the course of their affair. The resulting forecast for this couple is, tragically, a never ending cycle of love and hate. At least they manage to achieve simultaneous love a quarter of the time.
Romeo’s behavior can be modeled by the differential equation
⇒ dRdt = a J
which describes how his love (represented by R) changes in the next instant (represented by dt). According to this equation, the amount of change (dR) is just a multiple (a) of Juliet’s current love (J) for him. This reflects what we already know—that Romeo’s love goes up when Juliet loves him—but it assumes something much stronger. It says that Romeo’s love increases in direct linear proportion to how much Juliet loves him. This assumption of linearity is not emotionally realistic, but it makes the equations much easier to solve. Juliet’s behavior, by contrast, can be modeled by the equation
⇒ dJdt = -b R
The negative sign in front of the constant b reflects her tendency to cool off when Romeo is hot for her
Vectors:
To give a sense of what Maxwell accomplished and, more generally, what vector calculus is about, let’s begin with the word “vector.” It comes from the Latin root vehere, “to carry,” which also gives us words like “vehicle” and “conveyor belt.” To an epidemiologist, a vector is the carrier of a pathogen, like the mosquito that conveys malaria to your bloodstream. To a mathematician, a vector (at least in its simplest form) is a step that carries you from one place to another
Logarithms
We know Log 10 = 1, Log 100 = 2, Log 1000 = 3. The interesting part here is that the numbers inside the logarithms are growing multiplicatively, increasing tenfold each time from 10 to 100 to 1000 their logarithms grew additively increasing from 1 to 2 to 3. Our brain performs a similar trick when we listen to music. The frequencies of the notes in a scale –do, re, mi, fa, sol, la, ti, do – sound to us like they’re rising in equal steps. But objectively their vibrational frequencies are rising by equal multiples. We perceive pitch logarithmically.
Math behind Google search
The approach builds on ideas from linear algebra, the study of vectors and matrices. Whether you want to detect patterns in large data sets or perform gigantic computations involving millions of variables, linear algebra has the tools you need. Along with underpinning Google’s PageRank algorithm, it has helped scientists classify human faces, analyze the voting patterns of Supreme Court justices, and win the million-dollar Netflix Prize (awarded to the person or team who could improve by more than 10 percent Netflix’s system for recommending movies to its customers)
For a case study of linear algebra in action, let’s look at how PageRank works. And to bring out its essence with a minimum of fuss, let’s imagine a toy Web that has just three pages, all connected like this:
The arrows indicate that page X contains a link to page Y, but Y does not return the favor. Instead, Y links to Z. Meanwhile X and Z link to each other in a frenzy of digital backscratching. The approach taken by Larry Page and Sergey Brin, the grad students who cofounded Google, was to let webpages rank themselves by voting with their feet—or, rather, with their links. In the example above, pages X and Y both link to Z, which makes Z the only page with two incoming links. So it’s the most popular page in the universe. That should count for something. However, if those links come from pages of dubious quality, that should count against them. Popularity means nothing on its own. What matters is having links from good pages. Google’s algorithm assigns a fractional score between 0 and 1 to each page. That score is called its PageRank; it measures how important that page is relative to the others by computing the proportion of time that a hypothetical Web surfer would spend there. Whenever there is more than one outgoing link to choose from, the surfer selects one at random, with equal probability. Under this interpretation, pages are regarded as more important if they’re visited more frequently (by this idealized surfer, not by actual Web traffic)
And because the Page Ranks are defined as proportions, they have to add up to 1 when summed over the whole network. This conservation law suggests another, perhaps more palpable, way to visualize PageRank. Picture it as a fluid, a watery substance that flows through the network, draining away from bad pages and pooling at good ones. The algorithm seeks to determine how this fluid distributes itself across the network in the long run. The answer emerges from a clever iterative process. The algorithm starts with a guess, then updates all the Page Ranks by apportioning the fluid in equal shares to the outgoing links, and it keeps doing that in a series of rounds until everything settles down and all the pages get their rightful shares.
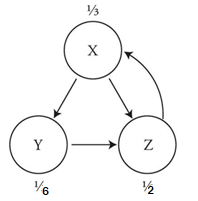
The value of the page rank of Z after update changes. The scores are updated to better reflect each page’s true importance. The rule is that each page takes its PageRank from the last round and parcels it out equally to all the pages it links to. Thus, after one round, the updated value of X would still equal 1/3, because that’s how much PageRank it receives from Z, the only page that links to it. But Y’s score drops to a measly 1/6, since it gets only half of X’s PageRank from the previous round. The other half goes to Z, which makes Z the big winner at this stage, since along with the 1/6 it receives from X, it also gets the full 1/3 from Y, for a total of ½.
Now we can happily correct our friends who say Math is useless!!
Disclaimer:
The wonderful book by Steven Strogatz has given many interesting points, which are being assembled by me in this summary. To do this I have used my discretion, personal examples to relate it to me in a better way.
Vinay Wagh
Bulls Eye.